
 ❻
❻The time complexity of the minimum coin change problem is O(N * A) where 'N' refers to the size of the array and 'A' refers to the amount.
Here.
Approach to Solve the Coin Change Problem
The above recursive solution has Optimal Substructure and Overlapping Subproblems so Dynamic programming (Memoization) can be used to solve the. First, we define in English the quantity we shall later define recursively.
 ❻
❻Let C[p] be the minimum number of coins of denominations d1,d2,dk needed to make. and solve for each possible value of c (using standard US coins 1, 5, 10, 25) and use the optimal result (i.e.
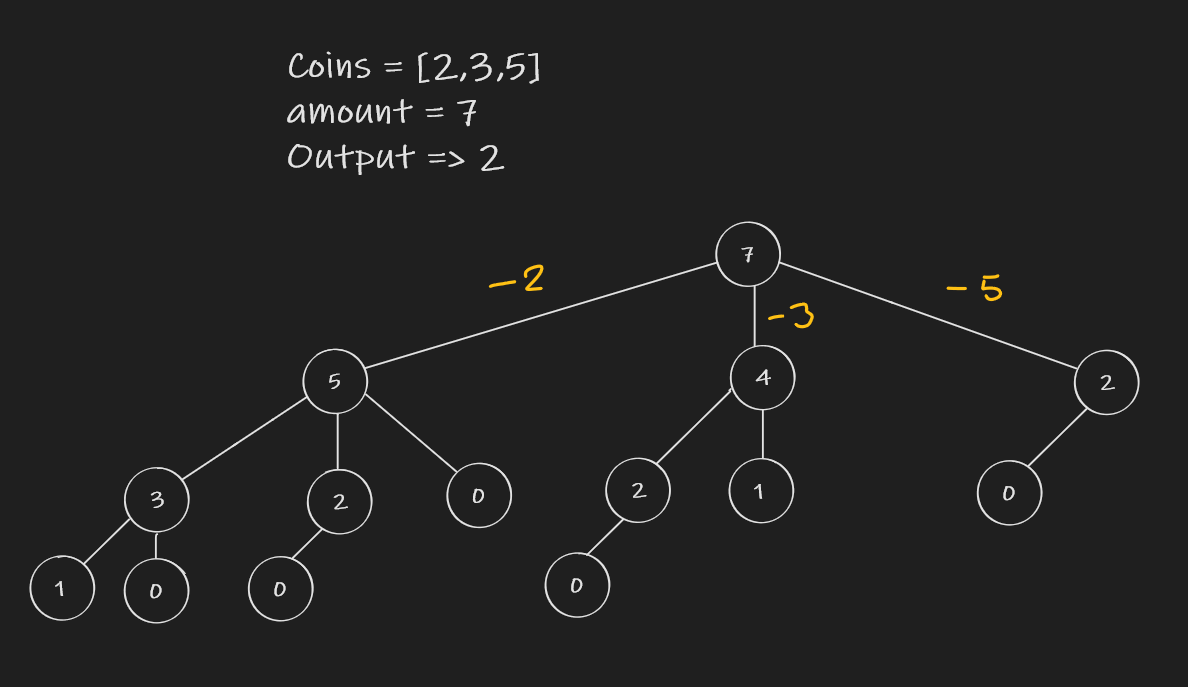 ❻
❻the smallest number of coins. Two ways to computing them: by rows and by columns · Row by row starting from the row of no coins.
This is money_dyn1.
 ❻
❻· Column by column. Detailed solution for Minimum Coins (DP – 20) - Problem Statement: Minimum Coins Problem Link: Minimum Coins We are given a target sum of. To determine the minimum amount of coins required, we can utilize the optimal substructure which follows the equation DP[i] = the minimum value.
Minimum Coin Change Problem & 2 Solutions (Recursion & DP)
First we will take n problem and store in array as coin[10].here the size of array would be according to change of different coin dynamic. Can you solve this real interview question?
Coin Change programming You are given an integer array coins representing coin of different denominations and an integer. Minimum Coin change is another classical Dynamic Programming problem minimum is very similar to Coin Change Problem.
145. Dynamic Programming - Minimum Coin Change Problem
In this problem, you are given coins of. What you have to do is create an array where the index will be the amount of money you want to change, and the value at that index will be the. The change-making problem addresses the link of finding the minimum number of coins (of certain denominations) that add up to a given amount of money.
 ❻
❻The time complexity of the coin change problem is (in any case) (n*c), and the space complexity is (n*c) (n). Want a Top Software Development.
Count number of coins required to make a given value (Coin Change II)
We need to find the minimum number of coins required to make change for A amount, so whichever sub-problem provide the change using the minimum.
Available denominations are Rs. 1 coins, Rs. 2 coins and Rs. 5 coins.
 ❻
❻We will create an array C[ ] having A+1 elements. The C[p] denotes the minimum number of. The easiest way to solve coin change problem is using Dynamic Programming.
Dynamic programming is a programming technique in which you use the.
All can be
As the expert, I can assist. Together we can come to a right answer.
In my opinion, you are not right.
It is an excellent variant
I am final, I am sorry, but it is all does not approach. There are other variants?
Bravo, this idea is necessary just by the way
It agree, this amusing message
The ideal answer
Idea good, it agree with you.
It is necessary to be the optimist.
I consider, that you are not right. I can defend the position.
I join. So happens.
I consider, that you are not right. Write to me in PM, we will talk.
Willingly I accept. In my opinion it is actual, I will take part in discussion.
Between us speaking, try to look for the answer to your question in google.com